Toàn bộ kiến thức về công tính, cách tính chu vi hình tam giác

Tam giác là hình học phổ biến mà chúng ta biết đến trong chương trình toán tiểu học. Cách tính chu vi hình tam giác? Cùng ôn lại kiến ​​thức môn Toán qua bài viết dưới đây nhé!

một hình tam giác là gì?

Trước khi tìm hiểu cách tính chu vi tam giác, hãy cùng tìm hiểu sơ qua về điểm, tính chất và nhóm tam giác nhé!

Tam giác là mặt phẳng một chiều có ba đỉnh có ba giao điểm; Ba đoạn thẳng chính là ba đoạn thẳng nối các đỉnh với nhau. Một tam giác quen thuộc là một đa giác có ít cạnh.

Tính chất tam giác: Xét ba ABC ta có:

• Tổng ba góc trong của một tam giác bằng 180 độ.

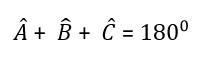
• Độ dài một cạnh lớn hơn hiệu hai cạnh và nhỏ hơn tổng hai cạnh. Đó là: AB – BC AC AB + BC
• Trong một tam giác, cạnh đối diện với góc nhọn sẽ là cạnh nhọn. Ngược lại, góc đối diện với cạnh lớn hơn sẽ lớn hơn.
• Ba chân trong tam giác sẽ bắt chéo (chéo qua) bề mặt. Điểm này được gọi là trực tâm của tam giác, hay điểm tọa độ.
• Ba kích thước trung tâm trong một tam giác đi qua một điểm, được gọi là trọng tâm của tam giác. Khoảng cách từ trọng tâm đến cạnh của tam giác bằng ⅔ độ dài từ trọng tâm đến cạnh đó.
• Ba đoạn vuông góc của tam giác cũng cắt nhau tại bề mặt. Điểm này là tâm đường tròn của tam giác.
• Ba thành phần bên trong đi qua một điểm duy nhất. Điểm này là tâm đường tròn của tam giác.

Tam giác đặc biệt:

• Tam giác cân
• Tam giác đều
• tam giác vuông
• Góc vuông của tam giác

Cách tính chu vi hình tam giác lớp 3

Công thức tính chu vi tam giác đều

* Đặc điểm của tam giác cố định:

• Có 3 cạnh có độ dài khác nhau
• Có ba góc có số đo khác nhau

* Công thức tính toán:

Để tính độ dài tam giác đều ta cần tính độ dài ba cạnh của tam giác.

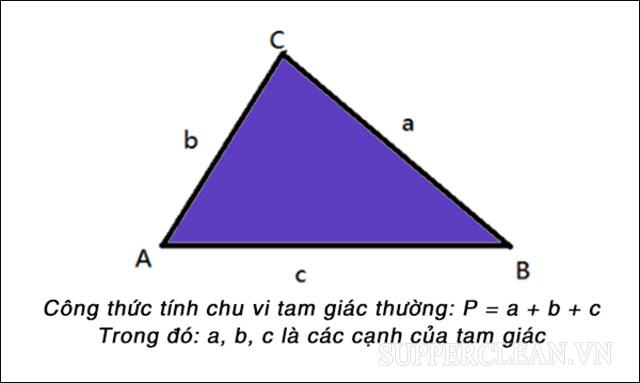
P = a + b + c

(P: chu vi tam giác; a, b, c lần lượt là độ dài ba cạnh của tam giác).

Từ đó xác định nửa diện tích tam giác và chia chu vi cho 2.

p = P/2

(p: nửa vòng)

Ví dụ 1: Cho tam giác ABC có các cạnh lần lượt là 7 cm, 10 cm, 12 cm. Tính chu vi tam giác? Tính nửa chu vi tam giác?

Hồi đáp:

Chu vi tam giác ABC là:

P = AB + BC + CA = 7 + 10 + 12 = 29 (cm)

Đường tròn ngoại tiếp tam giác ABC là:

p = P : 2 = 29 : 2 = 14,5 (cm)

Ví dụ 2: Tìm diện tích tam giác ABC và cạnh AB = 14cm. Độ dài các cạnh AC và BC dài hơn cạnh AB là 12 cm.

Hồi đáp:

Độ dài cạnh AC và BC là: 12 + 14 = 26 cm

Chu vi tam giác ABC là: AB + AC + BC = 14 + 26 = 40 cm

Cách tính chu vi tam giác cân?

* Tính chất của tam giác cân

• Có hai cạnh bên và hai góc ở đáy bằng nhau
• Trong một tam giác cân, đường trung tuyến bằng cạnh đáy sẽ là tia phân giác và là độ dài của tam giác cân.

* Vòng tròn:

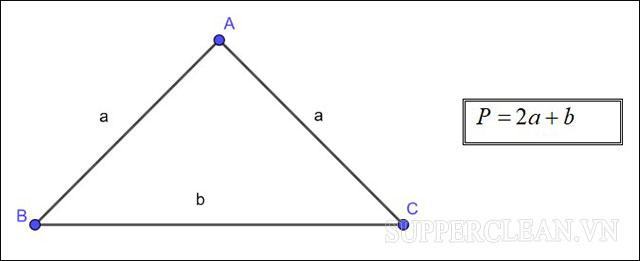
Xét tam giác cân ABC có cạnh AB = AC. Sau đó, chu vi của tam giác được xác định theo công thức sau:

P = AB + BC + AC trong đó AB = AC

=> P = 2AB + BC

Ví dụ: Cho tam giác ABC cân tại A, cạnh AB = 3cm, cạnh BC = 7cm. Tính chu vi tam giác?

Hồi đáp:

Vì tam giác ABC cân tại A nên AB = AC = 3cm.

Khi đó chu vi tam giác ABC là:

P = AB + BC + CA

= 3 + 7 + 3 = 13 (cm)

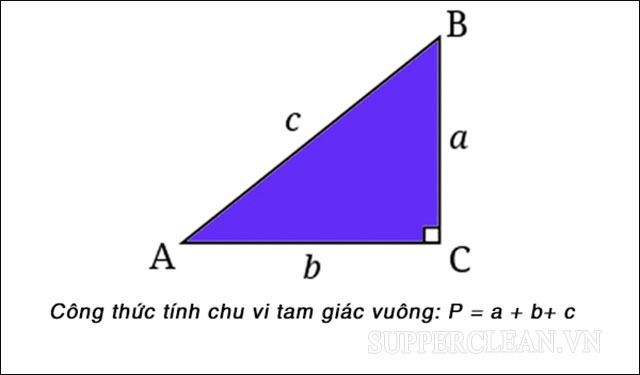
Cách tính chu vi tam giác vuông

Các dạng tam giác vuông:

• Có một góc vuông.
• Hai góc nhỏ của tam giác vuông bằng nhau.
• Đường thẳng của cạnh huyền bằng tổng bình phương hai cạnh góc (Định lí Python).
• Đường trung trực của một đoạn thẳng bằng nửa cạnh huyền.

* Bí mật:

Cũng như các tam giác khác, chu vi của tam giác vuông cũng được tính bằng tổng của 3 cạnh.

P = a + b + c

(P: chu vi: a, b, c lần lượt là độ dài ba cạnh của một tam giác vuông).

Ví dụ: Cho tam giác ABC có cạnh A. Cạnh AB dài 6 cm, cạnh AM dài 5 cm. Tính chu vi tam giác?

Hồi đáp:

Cho tam giác ABC, cạnh huyền nằm bên phải A, có:

• AB và AC là hai cạnh.
• BC là cạnh huyền

Sử dụng dạng tam giác vuông, ta có:

BC = 2AM = 2 x 5 = 10cm

Áp dụng định lý Pitago cho tam giác vuông, ta có:

AC2 = BC2 – AB2 = 100 – 36 = 64 (cm) => AC = 8cm

Vậy chu vi tam giác ABC là:

P = AB + BC + CA = 6 + 10 + 8 = 24cm

Cách tính chu vi tam giác cân?

* Tính chất của tam giác vuông cân

• Có một góc vuông và hai cạnh bên phải có độ dài bằng nhau.
• Hai góc nhọn trong một tam giác vuông bằng nhau và bằng 45 độ.
• Ngoài ra, nó có tất cả các thuộc tính và tính chất của tam giác cân và tam giác vuông.

* Vòng tròn:

P = a + b + c

(P: chu vi tam giác; a, b, c lần lượt là độ dài các cạnh của tam giác).

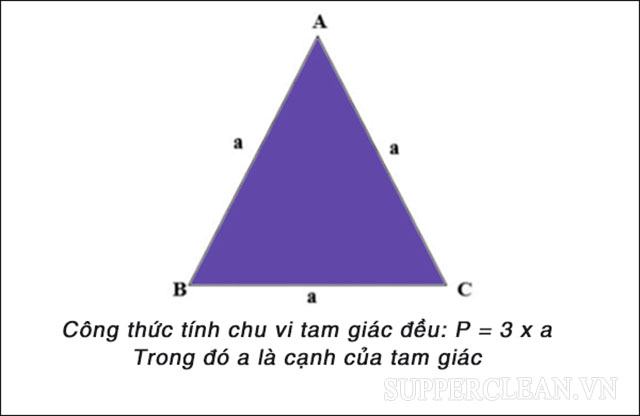
Cách tính chu vi tam giác đều?

Hình tam giác đều:

• Có 3 phần chung
• Có 3 góc bằng nhau bằng 60 độ.
• Trong tam giác đều, đường trung tuyến và độ dài là đường phân giác.

* Công thức tính toán:

Xét tam giác đều ABC cạnh a. Khi đó, chu vi của tam giác đều được xác định bởi:

P = a + a + a = 3a

Ví dụ: Tìm diện tích tam giác nếu độ dài một cạnh là 6cm?

Hồi đáp:

Chu vi tam giác trên là:

P = 3a = 3 x 6 = 18cm

Tham khảo: Cách tính diện tích hình thang đều, vuông, cân | Toán 5, 6

Trên đây là bài viết tổng hợp các phương pháp tính chu vi hình tam giác. Khi làm bài nhớ thay đổi thông số tương tự để đọc chính xác nhất nhé!

Bạn thấy bài viết Toàn bộ kiến thức về công tính, cách tính chu vi hình tam giác có khắc phục đươc vấn đề bạn tìm hiểu ko?, nếu ko hãy comment góp ý thêm về Toàn bộ kiến thức về công tính, cách tính chu vi hình tam giác bên dưới để Trường Đại học Đại Việt Sài Gòn có thể thay đổi & cải thiện nội dung tốt hơn cho các bạn nhé! Cám ơn bạn đã ghé thăm Website: daihocdaivietsaigon.edu.vn của Trường Đại học Đại Việt Sài Gòn

Nhớ để nguồn bài viết này: Toàn bộ kiến thức về công tính, cách tính chu vi hình tam giác của website

Chuyên mục: Hỏi đáp