R là tập hợp số gì? Bài tập về hàm số đồng biến – nghịch biến trên R

Số R là gì? Hàm nghịch biến đồng biến trên R là gì? Hãy cùng superclean.vn kiểm tra phép toán này trong bài viết dưới đây nhé!

Số R là gì?

Tập hợp R là gì?

Trong toán học, R là ký hiệu cho các số thực, bao gồm cả số hữu tỷ và số vô tỷ. R là số lớn nhất trong toán học.

R là viết tắt của số thực

Trong môn toán lớp 10, chúng ta được học dạng toán sau:

• Tập hợp các số tự nhiên N : N = {0, 1, 2, 3, 4, 5,….}
• Bộ Z : Z = {….., –3, -2, -1, 0, 1, 2, 3,….}
• Nhóm các số hữu tỉ Hỏi: Đây là những số mà chúng ta có thể biểu diễn dưới dạng tỉ số a/b. Trong đó a và b đều là số và b#0. Ví dụ: 1/2, 3/2, 6/5, v.v.
• Tập hợp các số vô tỉ I: Số thập phân không lặp lại. Ví dụ: số π, √2, √3,…

Từ đó, ta có mối quan hệ giữa các số trên như sau:

• N ⊂ Z; Z ⊂ Q; QR, IR và QI = hoặc N ⊂ ZQR
• R = Q tôi

Tập hợp các số trong toán học

Số rẻ thật

Mỗi số thực được biểu diễn bằng một điểm trên trục số. Ngược lại, mỗi điểm trên trục số biểu diễn một số thực.

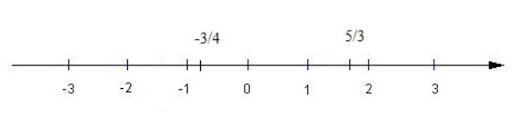
Một số thành phần của nhóm số thực:

Trong đó:

• Dấu (- ) được đọc như sau: chú ý tiêu cực hoặc chú ý liên tục
• Dấu (+∞) đọc là: dương vô cực hay dương vô cực.

Tính chất của số thực

Cũng như các tập hợp số khác, ta có thể thực hiện các phép tính như trừ, cộng, chia, nhân, biểu thức hay nghiệm của R. Ta có thể chứng minh như sau:

Với mọi số a thuộc R, ta có: a + 0 = a.

Cho các số a, b thuộc R, ta có: a + b = b + a.

Tương tự với các số a, b, ca R, ta có: a + c = b + c => a = b.

Như vậy ta thấy các hàm của R là hằng hoặc nguyên như đối với các bộ số khác. Bạn cũng có thể xác minh tương tự cho phép trừ, phép nhân, phép chia, v.v.

Ta cũng có các số thực sau:

• Mọi số thực khác 0 đều dương hoặc âm.
• Tổng hoặc tích của hai số thực không âm sẽ là một số thực không âm.
• Tập hợp các số thực là một số thực vô hạn, không đếm được.

Ví dụ về số thực

R là viết tắt của số thực, có cả số hữu tỷ và số vô tỷ. Ngoài ra, chúng ta có mối quan hệ sau giữa các số toán học: N ⊂ Z ⊂ Q ⊂ R.

Ví dụ về số thực: -5; -3, 3, 2, 1, 5/2, 3/2, √2,…

R trong hình học là gì?

Không chỉ là một ký hiệu trong đại số, r và R được sử dụng trong hình học. R và r lần lượt được dùng để biểu thị bán kính của hình tròn và chu vi của tam giác.

Cách tính bán kính hình tròn

* Cách 1: Sử dụng định lý sin trong tam giác

Cho tam giác ABC có BC = a, AC = b, AB = c và R là chu vi của tam giác ABC trên. Tại thời điểm này, chúng tôi có:

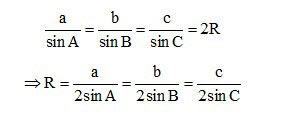
* Cách 2: Sử dụng công thức tính diện tích tam giác

Cho tam giác ABC có BC = a, AC = b, AB = c và R là chu vi của tam giác ABC trên. Tại thời điểm này, chúng tôi có:

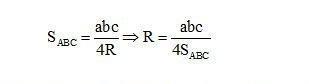
Tính chu vi đường tròn nội tiếp

Cho tam giác ABC có BC = a, AC = b, AB = c và r là bán kính của tam giác ABC trên. Vì vậy chúng tôi có:

Bán nguyệt tam giác ABC: p = (a + b + c)/2.

Diện tích tam giác ABC: S = p * r

Từ đó, ta có:

r = S/p

Ví dụ về cách tính chu vi tam giác:

Ngoài ra, r còn xuất hiện trong công thức tính diện tích và tính chu vi hình tròn với r là bán kính hình tròn:

• Chu vi hình tròn: C = d.π = 2rπ
• Diện tích bề mặt: S = r2π.

Hàm số đồng biến trên R và hàm số nghịch biến trên R là gì?

Để xét tính đơn điệu (đồng biến hoặc nghịch biến) của một hàm số liên tục R, điều đầu tiên là hàm số đó phải xác định trên R.

Tùy thuộc vào một vấn đề cụ thể, chúng tôi sẽ có giá trị null trên R cho các chức năng khác nhau. Như sau:

* Đa thức bậc 1: y = ax + b (a#0)

* Hàm đa thức bậc 3: y = ax3+ bx2+ cx + d (a#0)

Ta có: Kết quả đầu tiên của hàm này như sau: y’ = 3ax2+ 2bx + c

* Đa thức bậc chẵn không thể là số ít trên R.

Để hiểu rõ hơn về các chức năng của R, chúng ta sẽ làm như sau:

Ví dụ 1: Hàm số nào sau đây đồng biến trên R?

Ví dụ 2: Hàm số nào sau đây đồng biến trên R?

Ví dụ 3: Tìm giá trị của m để hàm số đồng biến trên R?

Ví dụ 4: Tìm giá trị của m để hàm số khả vi trên R?

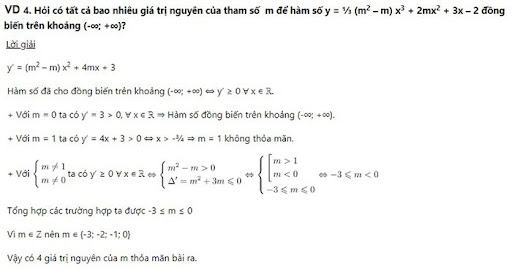
Bài viết tham khảo: Tiếng Anh là gì? Tầm quan trọng của ngôn ngữ ngày nay

Hi vọng với những thông tin cung cấp trên đây đã giúp bạn hiểu R là nhóm số gì và một số dạng biến cố liên quan đến hàm số đồng biến, hàm số đồng biến trên R. Nếu còn thắc mắc, hãy đặt câu hỏi về hàm số đồng biến. nội dung về chủ đề, hãy để lại bình luận bên dưới bài viết này, chúng tôi sẽ giúp bạn phản hồi trong thời gian sớm nhất!

Bạn thấy bài viết R là tập hợp số gì? Bài tập về hàm số đồng biến – nghịch biến trên R có khắc phục đươc vấn đề bạn tìm hiểu ko?, nếu ko hãy comment góp ý thêm về R là tập hợp số gì? Bài tập về hàm số đồng biến – nghịch biến trên R bên dưới để Trường Đại học Đại Việt Sài Gòn có thể thay đổi & cải thiện nội dung tốt hơn cho các bạn nhé! Cám ơn bạn đã ghé thăm Website: daihocdaivietsaigon.edu.vn của Trường Đại học Đại Việt Sài Gòn

Nhớ để nguồn bài viết này: R là tập hợp số gì? Bài tập về hàm số đồng biến – nghịch biến trên R của website

Chuyên mục: Hỏi đáp