[Hướng dẫn] Cách tính diện tích tam giác thường – vuông – cân

Bạn đang muốn tính diện tích tam giác dùng trong học tập. Vậy hãy tham khảo bài viết chia sẻ dưới đây của chúng tôi nhé!

Học cách tính diện tích tam giác

một hình tam giác là gì?

Tam giác là một hình học quan trọng; nó có 3 đỉnh là 3 điểm không thẳng hàng và 3 cạnh là 3 đường thẳng nối 3 điểm đó. Tam giác là đa giác có ít cạnh hơn. Đó là một đa giác đều và một đa giác nằm ngang trong đó các góc trong luôn nhỏ hơn 180 độ.

Một nhóm tam giác

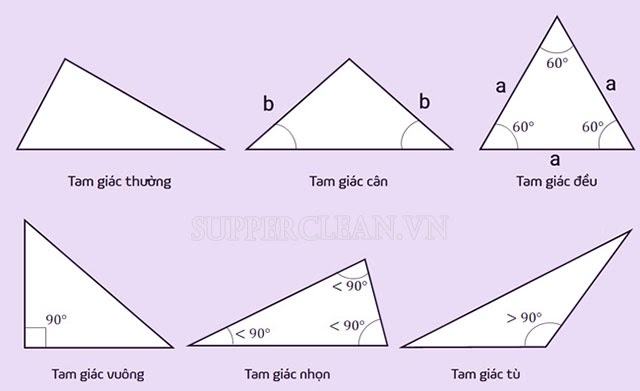
• Một tam giác bình thường: Đây là loại hình tam giác cơ bản nhất; chúng có chiều dài cạnh khác nhau và kích cỡ khác nhau.
• Tam giác cân: Một tam giác có hai cạnh dài bằng nhau. Góc của tam giác cân là giao điểm của hai cạnh. Góc tạo bởi đỉnh gọi là góc ở đỉnh, hai góc còn lại gọi là góc ở đáy. Cho một góc cân, hai góc chính có số đo bằng nhau.
• Tam giác đều: Đây là trường hợp đặc biệt của tam giác cân có ba cạnh bằng nhau. Theo hình dạng của một tam giác đều, ba góc của một tam giác có cùng số đo và bằng 60º.

Các loại hình tam giác

• Tam giác vuông: Đây là tam giác có số đo một góc là 90º, góc này vuông. Cạnh đối diện với góc vuông là cạnh có số đo lớn nhất gọi là cạnh huyền. Hai cạnh còn lại gọi là hai cạnh của góc vuông.
• Ba góc nhọn: Đây là những hình tam giác có các góc bên trong nhỏ hơn 90º. Nói cách khác, tam giác nhọn là tam giác có các góc ngoài lớn hơn 90º.
• Hình tam giác: Tam giác có góc trong (lớn hơn 90º) hoặc góc ngoài bằng góc ngoài (nhỏ hơn 90º).
• Tam giác vuông: Đó là tam giác cân và tam giác vuông. Dạng tam giác vuông cân thì hai cạnh của góc vuông có độ dài bằng nhau; Hai góc có cùng số đo và bằng 45º.

Cách tính diện tích tam giác?

Các phương pháp tính diện tích tam giác thường

* Công thức chung

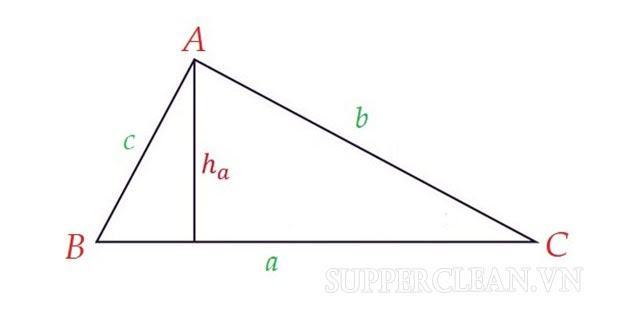
Giải thích: Diện tích của một tam giác thường được xác định bằng cách nhân độ dài từ một đỉnh với độ dài cạnh còn lại của đỉnh đó rồi chia kết quả cho 2. Nói cách khác, diện tích của tam giác. Nó thường được tính bằng ½ hệ số độ dài từ đỉnh xuống dựa trên độ dài của cạnh còn lại của đỉnh.

Gọi ha, hb, hc lần lượt là độ dài các đoạn thẳng kẻ từ các đỉnh A, B, C của tam giác ABC. Sau đó, chúng ta có công thức này:

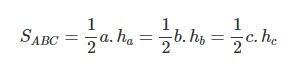
Ví dụ: Một hình tam giác có chiều dài 5cm. Chiều cao tương ứng là ¾ chiều cao tầng. Tính diện tích tam giác?

Hồi đáp:

• Chiều dài tam giác = × 5 = 3,75cm
• Diện tích hình tam giác = × (3,75 × 5) = 9,375 cm2

* Tính diện tích tam giác khi biết số đo một góc

Định nghĩa: Diện tích tam giác bằng ½ tích hai cạnh kề với sin của góc tạo bởi hai cạnh đó. Công thức:

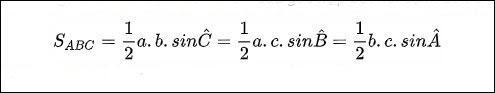
Ví dụ: Tam giác ABC có cạnh CB = 5cm, cạnh CA = 8cm và góc BCA có 63 số đo.

Hồi đáp:

Diện tích tam giác ABC = × 5 × 8 × sin BCA = × 5 × 8 × = 10 cm2

* Tính diện tích tam giác có ba cạnh (công thức Heron)

Gọi p là nửa đường tròn của tam giác ABC. Sau đó, chúng ta có công thức này:

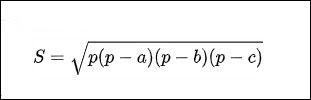
Mặt khác:

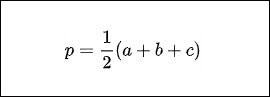
Từ đó, công thức trên có thể được viết lại như sau:

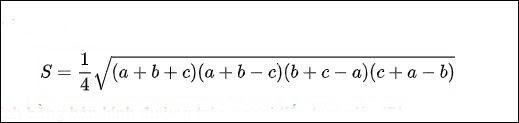
Ví dụ: Một tam giác có độ dài ba cạnh lần lượt là 8cm, 9cm, 10cm. Tính diện tích tam giác.

Hồi đáp:

• Nửa chu vi tam giác = (8 + 9 + 10)/2 = 13,5cm
• Diện tích hình tam giác = √13,5 × (13,5- 8) × (13,5 – 9) × (13,5 – 10) = 13,5 cm2.

* Tính diện tích tam giác dựa vào chu vi tam giác

Gọi R là bán kính của tam giác ABC. a, b, c lần lượt là độ dài các cạnh của tam giác. Chúng ta có:

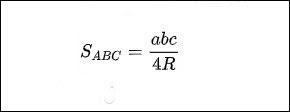
Xác nhận:

Ngoài ra, bạn cũng có thể tính diện tích tam giác ABC bằng phương pháp này:

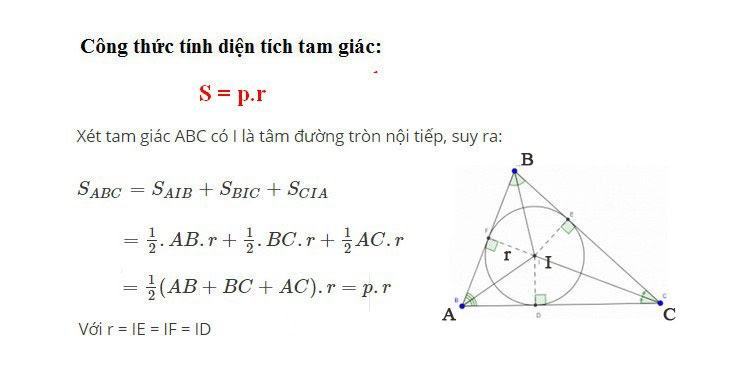
* Tính diện tích tam giác dựa vào độ dài đường tròn nội tiếp

Gọi r là chu vi tam giác ABC và p là nửa diện tích tam giác ABC. Khi đó, công thức tính như sau:

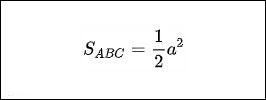
Công thức đã được chứng minh:

Cách tính diện tích tam giác đều?

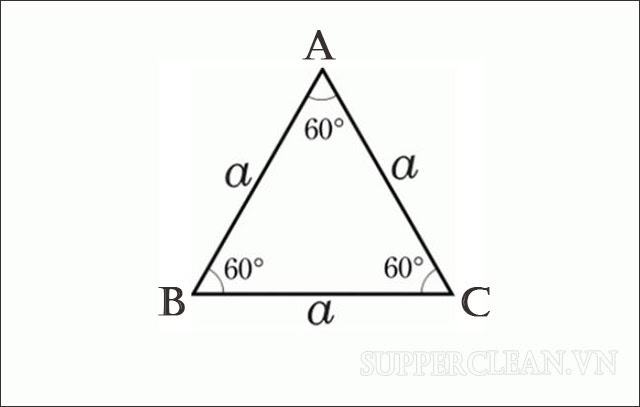
Cho tam giác đều ABC có độ dài các cạnh như hình vẽ. Từ đó ta có công thức tính diện tích như sau:

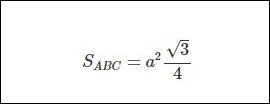
Công thức tính diện tích tam giác cân

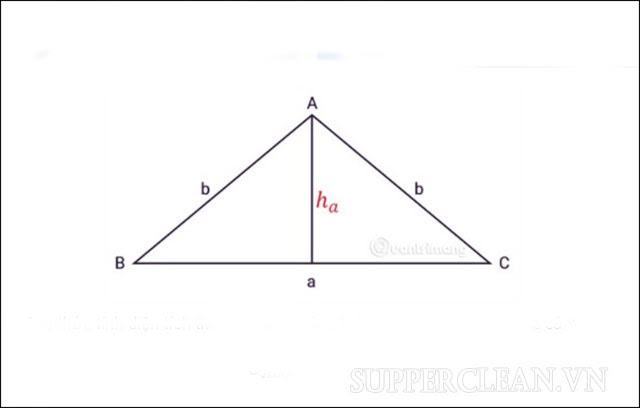
Xét tam giác cân ABC như hình bên, ta có: ha là độ dài từ đỉnh tam giác đến đáy có độ dài a. Chúng tôi có công thức này:

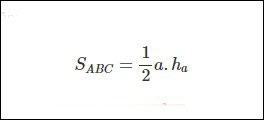
Tính diện tích tam giác vuông

Giải thích: Tính diện tích tam giác vuông cũng giống như tính diện tích tam giác thường; nó được định nghĩa là ½ hệ số chiều cao và chiều cao bằng với đáy. Tuy nhiên, trong một tam giác vuông, bạn không cần tính độ dài của tam giác vì một cạnh của góc vuông sẽ là độ dài và cạnh còn lại sẽ là đáy.

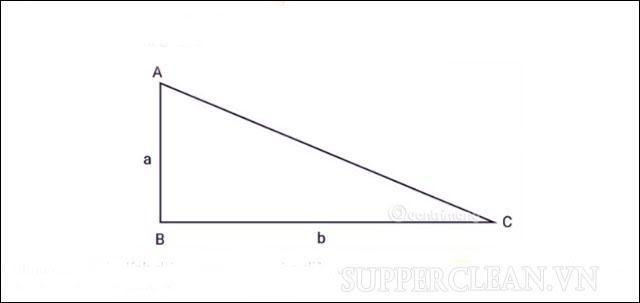
Gọi a, b là độ dài hai cạnh của tam giác vuông ABC. Chúng ta có:

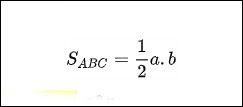
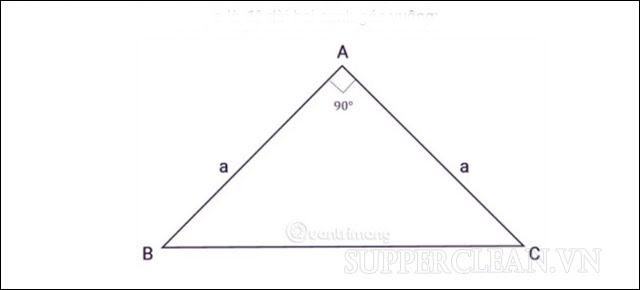
Cách tính diện tích tam giác cân?

Từ công thức tính diện tích tam giác vuông và tam giác cân ta có công thức tính diện tích tam giác vuông cân này:

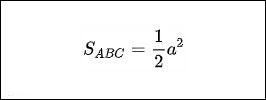
Chúng tôi hi vọng với những cách tính diện tích tam giác lớp 8 sẽ mang đến cho các em học sinh những thông tin hữu ích. Đừng quên luyện tập mỗi ngày để đạt kết quả cao nhất trong phần hình học này nhé!

Người trình bày: [Hướng dẫn] Cách tốt nhất để đổi độ F sang độ C và ngược lại

Bạn thấy bài viết [Hướng dẫn] Cách tính diện tích tam giác thường – vuông – cân có khắc phục đươc vấn đề bạn tìm hiểu ko?, nếu ko hãy comment góp ý thêm về [Hướng dẫn] Cách tính diện tích tam giác thường – vuông – cân bên dưới để Trường Đại học Đại Việt Sài Gòn có thể thay đổi & cải thiện nội dung tốt hơn cho các bạn nhé! Cám ơn bạn đã ghé thăm Website: daihocdaivietsaigon.edu.vn của Trường Đại học Đại Việt Sài Gòn

Nhớ để nguồn bài viết này: [Hướng dẫn] Cách tính diện tích tam giác thường – vuông – cân của website

Chuyên mục: Hỏi đáp